Sandra Nestler
Dr. rer. nat.
Postdoctoral Fellow with Prof. Omri Barak at Technion – Israel Institute of Technology

Multi-Task learning
Human behavior is closely linked to our ability to solve multiple tasks, which serve as basic building blocks for more complex behaviors. However, prevailing neuroscientific research often focuses on single-task learning to examine individual phenomena in detail. Yet, understanding joint effects between tasks is crucial as they provide insights into currently underexplored areas like resource sharing, task interference, and how a learned task, in form of its neural representation, is retained in the network throughout further development.
In this project, we therefore investigate multi-task learning, particularly how learning one task influences the representation of another. There are two features of neural networks that may underlie learning: The network structure in form of its connectivity and the neural activity propagating along it. We study both alongside one another by measuring the neural activity and approximating the connection weights with correlations. By bridging theoretical frameworks with empirical observations, this research aims to advance our understanding of neural dynamics in multi-task environments.

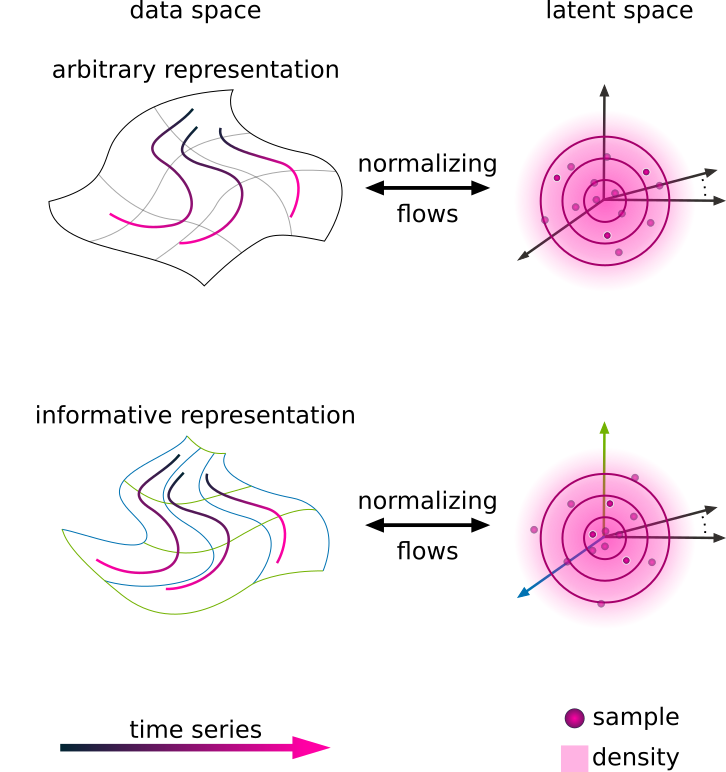
Manifold learning with Normalizing Flows
Despite the large number of active neurons in the cortex, the activity of neural populations for different brain regions is expected to live on a low-dimensional manifold. Variants of principal component analysis (PCA) are frequently employed to estimate this manifold. However, these methods are limited by the assumption that the data conforms to a Gaussian distribution, neglecting additional features such as the curvature of the manifold. Consequently, their performance as generative models tends to be subpar.
To fully learn the statistics of neural activity and to generate artificial samples, we use Normalizing Flows. These neural networks learn a dimension-preserving estimator of the probability distribution of the data. They differ from other generative networks by their simplicity and by their ability to compute the likelihood exactly.
Our adaptation of NFs focuses on distinguishing between relevant (in manifold) and noise dimensions (out of manifold). Our adaptation allows us to estimate the dimensionality of the neural manifold. As every layer is a bijective mapping, the network can describe the manifold without losing information – a distinctive advantage of NFs.
Learning Interacting Theories from Data
Claudia Merger, Alexandre René, Kirsten Fischer, Peter Bouss, Sandra Nestler, David Dahmen, Carsten Honerkamp, and Moritz Helias
Phys. Rev. X 13, 041033
2023
Statistical temporal pattern extraction by neuronal architecture
Sandra Nestler, Moritz Helias, and Matthieu Gilson
Phys. Rev. Research 5, 033177
2023
Statistical physics, Bayesian inference and neural information processing
Erin Grant, Sandra Nestler, Berfin Şimşek and Sara Solla
arXiv:2309.17006v1
